Edited on Dillinger
映射
- 映射,或者射影:
- 两个非空集合A与B间存在着对应关系f,而且对于A中的每一个元素a,B中总有有唯一的一个元素b与它对应,就这种对应为从A到B的映射,记作f:A→B。其中,b称为元素a在映射f下的象,记作:b=f(a)。a称为b关于映射f的原象。集合A中所有元素的象的集合称为映射f的值域,记作f(A)。
- 函数:从非空数集到非空数集的映射,而且只能是一对一映射或多对一映射。(一个x只能对应一个y,但多个x可以对应一个y)
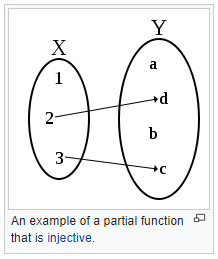
- partial function:
- 对于X中的值,可以有x1在Y中找不到相应的映射。(X中有一些x没有对应的y值)
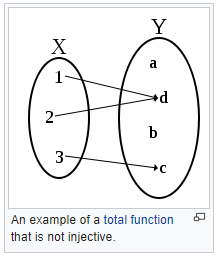
- total function:
- X中所有的值,xi在Y中都能找到相应的映射。(X’=X,X中所有x都有对应的y值)
-
- 单射(injective)
- 设f是由集合A到集合B的映射,如果所有x,y∈A,且x≠y,都有f(x)≠f(y),则称f为由A到B的单射。
- 不同的x映射到不同的y值。
- 不一定是total function。
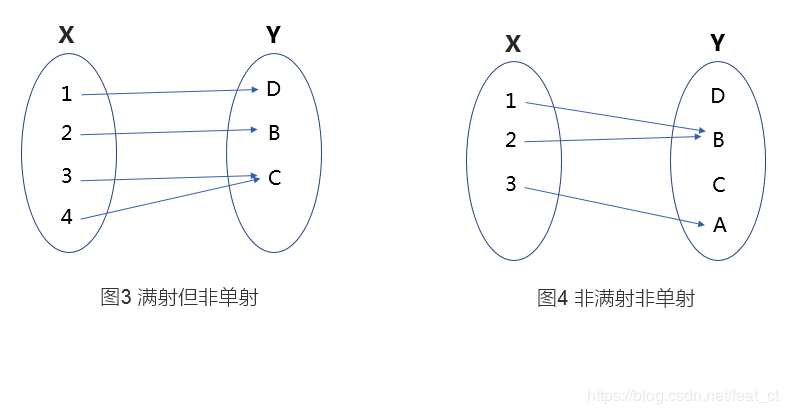
- 满射(surjection、onto,or 盖射)或称满射函数或映成函数
- 一个函数为满射,则对于任意的陪域Y中的元素 y,在函数的定义域X中存在一点 x使得f(x)=y。
- 指陪域等于值域的函数。
- 即:对陪域中任意元素,都存在至少一个定义域中的元素与之对应。
- 不一定是total function。
- 双射(bijective,or一一对应)
- 既是单射又是满射的函数。
- 即:一个双射函数形成一个对应,并且每一个x都有正好一个y以及每一个输出值都有正好一个输入值。
- 不一定是total function。
- 单射、双射、满射的总结:
- 设f是从集合A到集合B的映射,若f(A)=B,即B中任一元素b都是A中某元素的像,则称f为A到B上的满射;
- 若对A中任意两个不同元素a1不等于a2,它们的像f1不等于f2,则称f为A到B的单射;
- 若映射f既是单射,又是满射,则称映射f为A到B的“双射”(或“一一映射”)。
- 函数为双射当且仅当每个可能的像有且仅有一个变量与之对应。
References:
https://www.cnblogs.com/marsggbo/p/10129075.html
